All That Matters

We are all familiar with the basic ways in which light interacts with matter, when light absorption  causes atoms to move and creates heat, or when light gets absorbed by the outer electrons of atoms so that they move into energetically excited states, which is how electricity in solar cells is created. Common to both examples is that light is mainly used as an energy source, and it is easy to visualize. When scientists draw such light interactions into the energy diagram of say a molecule, they often draw little wavy arrows from one energy state to another.

But that’s the boring stuff. Far more interesting is that light can also strongly couple to matter, but without getting absorbed. The example I am discussing here is when the interaction between light and a molecule is so strong that it profoundly alters the molecule’s energy states themselves, and not merely lifts electrons from one state to another. In particular, what Thomas Ebbesen, Tal Schwartz, James Hutchison and colleagues at the University of Strasbourg have now shown is that such interactions could find exciting new applications: to control energy levels of molecules, and in this way to influence the kinetics of  chemical reactions in a new way that creates many new possibilities.

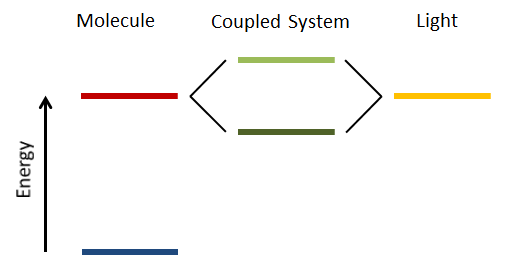
Strong coupling of light and matter. Light confined between two mirrors can strongly interact between matter that is also between the mirrors and has a matching energy level. The strong light-matter coupling then causes a splitting of the matching energy level into two separate states.

To see how this looks in practice it is necessary to understand what the strong coupling between light and molecules means. First of all, to achieve the necessary strong coupling, it is necessary to create a strong feedback mechanism between light and matter. This can be done by squeezing the light field between two closely spaced mirrors, with the desired molecules in-between. In addition, the energy levels of the light field between the mirrors and one of the energy levels of the molecule need to match up. If all these conditions are fulfilled, then the energy state in question is split into two separated states (see figure). This is called Rabi splitting. The stronger the coupling, the larger the energy separation between the two states. Because of the beauty of quantum mechanics this doesn’t even require light to be present, the mirrors are enough. […]

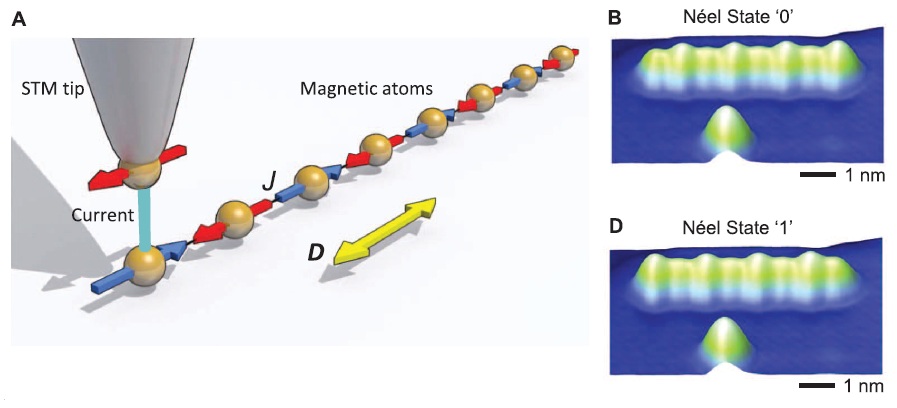
Information stored by a chain of magnetic atoms. Left: an STM tip measures the magnetic state of the iron atoms. Right: through increasing the current between tip and atoms the magnetic states can be switched. Peaks become valleys and vice versa. (c) Science Magazine

I now finally got the time to follow-up on last week’s paper in Science by Andreas Heinrich‘s group at IBM on magnetic storage elements that are only a few atoms in size. There have been a few misconceptions in some of the news reports with some being plainly wrong (‘smallest storage device ever made’), and many didn’t mention much about the scientific principles behind this study, although these are quite interesting. One of the better reports appeared in the New York Times, albeit again without going much into details. So I hope I can still add something useful with this blog post.

And actually, we’ve come across Andreas Heinrich’s previous research before, he does very innovative research with scanning tunneling microscopes (STM). In this latest Science paper he has now explored the limits of magnetic storage devices. Magnetism is of course the basis for storage such as magnetic hard drives. The problem in increasing the storage density in any magnetic storage device is that the magnetic regions begin to interfere with each other as they become smaller and are integrated closer together, because magnetic states on the order of just a couple of atoms are not very stable. […]

Symphonies are some of the most complex musical pieces. They involve different instruments, each with their own unique sound, and each instruments section playing their own tunes. Yet, what are symphonies in comparison to the complexity of life? Proteins for example, they are made of a limited number of building blocks, amino acids, but take highly complex shapes and assume a broad range of functions in the body.

Still, there is a commonality underlying such complex systems, in many cases they are hierarchical, which means they’re made of different objects on different scales – instruments playing tunes, amino acids forming proteins and so on. As David Spivak, Markus Buehler and others from MIT have described in a recent paper, a mathematical approach, known as category theory, can be used as a versatile tool that is capable of modelling complex systems by using the underlying rules governing a structure’s components. This is a very powerful approach and there is a lot to be gained by using this mechanism in materials science, to describe biomolecules or other hierarchical materials. Moreover, their approach makes it easy to connect different complex system. To put it crudely, understanding a Beethoven symphony may also provide insights into the properties of a protein, because category theory helps us links various complex systems.

Photo by Wayne Dixon via flickr.

To understand how this works, let’s take a look at an example provided by Buehler and colleagues – spider webs. These are made of individual fibres, consisting of smaller fibrils. The fibrils are made of a nanocomposite of crystal-like structures connected by flexible links. These structures are in turn made of various amino acids.

The complex structural hierarchy of spider silk (and other systems) is of course well-known. The problem researchers face is, however, that knowing the individual components of a material doesn’t necessarily mean that the properties of  the full system are known. For example, even though the molecular composition of a protein may be known, predicting its three-dimensional shape is notoriously difficult. It is the behaviour of structural elements in the context of their use that can be so difficult to understand. And this is where category theory is useful. […]