All That Matters

I used to laugh at those TV series and movies where crime investigators could take a surveillance camera photo, however fuzzy and blurred, and enhance its resolution beyond belief to the point where every possible (and impossible) detail becomes visible. I stopped laughing last week at a conference when I became aware of a 2009 study by Moti Segev and colleagues from Technion in Israel that demonstrates an amazing precision in the recovery of objects from imperfect images. The resolution they achieve is better than what even the best photographic lens can ever hope to image.

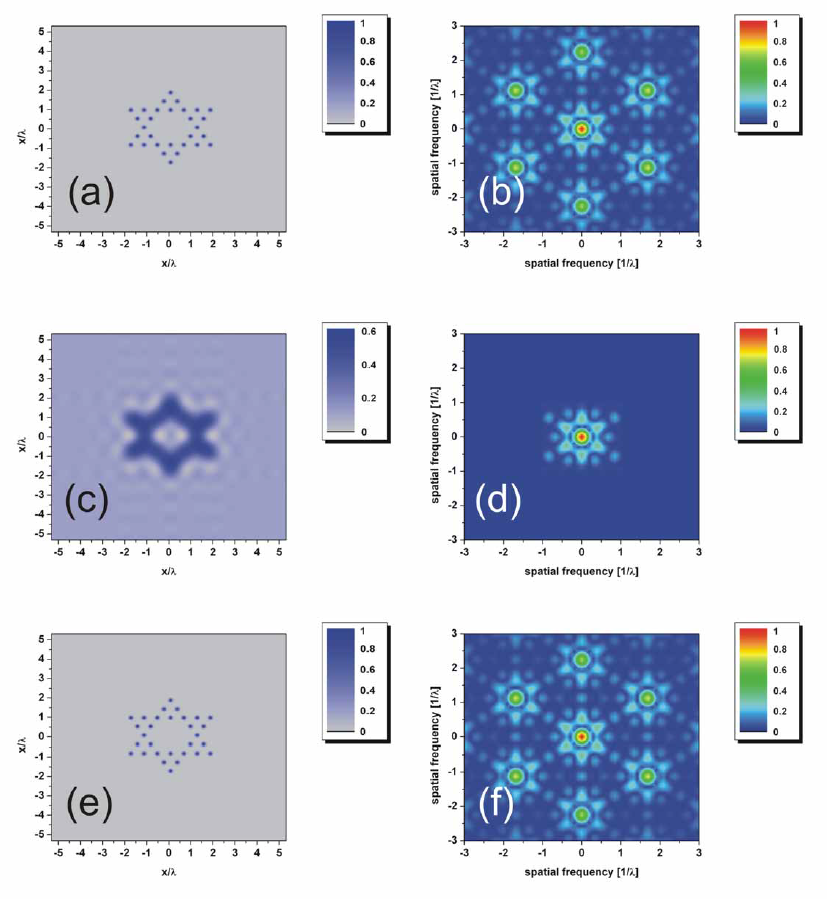
Enhancing image resolution. The top row shows the original object, both the image and its corresponding map showing the different frequencies that make up the image. Middle: the image as it would look like with the best resolution available with optical systems. Bottom: the reconstructed image. (c) Optics Express 17, 23920 (2009)

The notion of such an enhancement seemed so unbelievable at first because there is a maximum in resolution that a classical optical imaging system can deliver. This limit is about half of the wavelength of the light beams used. Any features smaller than this limit simply will not resolve however good the camera lens. Yet Segev and colleagues are easily able to beat this limit – without using any special equipment.

The reason for this limitation is that some of the light – the part that carries the information about the smallest features of an object – is absorbed by the medium through which light travels. Eventually, key information is missing from the image, and no exact mathematical reconstruction is possible.

How do you then reconstruct an image with high resolution? One option is to reconstruct the original object by making assumptions about the information that is missing. For example, if you know that a blurry image consists of the letters of the alphabet it becomes easier to guess the original. But such solutions are always restricted to certain circumstances and are also quite susceptible to noise in images.

[…]